Considerations in Mechanical Reliability

In Logistics Engineering and Management, logistics engineering pioneer Benjamin Blanchard defined Reliability as the probability that a system or product will perform its intended function in a satisfactory manner for a given period of time when used under specified operating conditions. Similarly, reliability engineering emphasizes satisfactory performance over a product’s lifecycle. To be an effective reliability engineer requires an understanding of failure mechanisms from experience and applied knowledge, as well as possessing a basic level of competency across engineering disciplines. “Reliability is, after all, engineering in its most practical form,” stated by James R. Schlesinger, Former U.S. Secretary of Defense.

In the past, items were made more reliable by over designing them. This process mitigated the need to understand dominant failure modes and material characteristics. Today, mechanical reliability is viewed much differently. The present-day designer is not afforded the luxury of over-engineering due to demanding customer requirements, the criticality of weight (particularly in aircraft), and product cost.

The current reliability engineering environment is made complex by the existence of a myriad of analysis and prediction approaches. These different approaches stem from the availability of advanced materials data and statistical modeling techniques using various software tools and computational advantages. Different approaches also apply multiple factors that can better model considerations such as manufacturing quality, material variations, system complexity, and design tolerances. To manage today’s reliability engineering efforts, we propose an approach that employs the Systems Engineering philosophy and quickly narrows focus to only those analysis activities that provide the insights desired by our program.

TRADITIONAL ANALYSIS METHODOLOGY

Typical program requirements utilize MIL-STD documentation as guidance for developing fielded reliability estimates or predictions. The reliability analysis process, presented in Figure 1, includes the estimated life or test program scope that considers reliability over a distribution of failures and typically involves the following steps:

1. 1. 1. 1. Understand the design requirements
         2. Characterization of the system and its hardware configuration
         3. Define the system operating conditions
         4. Define the system utilization rate/mission profile
         5. Establish reliability prediction method(s)
         6. Perform reliability prediction
         7. Summarize results and highlight conclusions

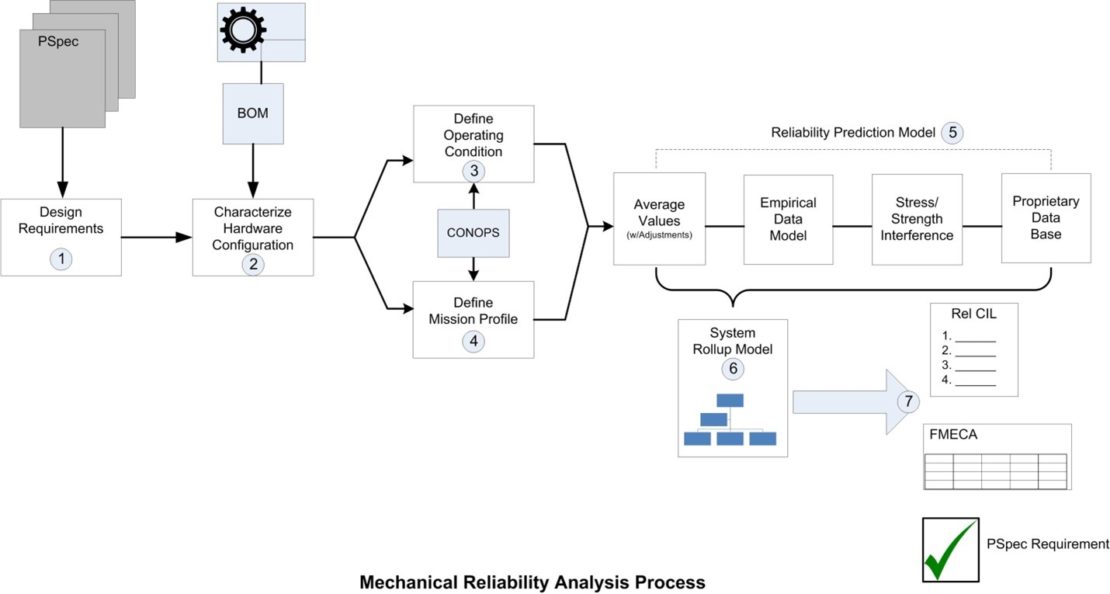
Step 5, “Establish reliability prediction method(s)”, presents a particular challenge for mechanical component reliability analysis. For electronic items, there exist analytical models that characterize the basic reliability of each  component type, and include adjustments for operating conditions (pi factors). The most notable is MIL-HDBK-217, Reliability Prediction of Electronic Equipment. There are also multiple software tools that implement the MIL-HDBK-217 methodology.

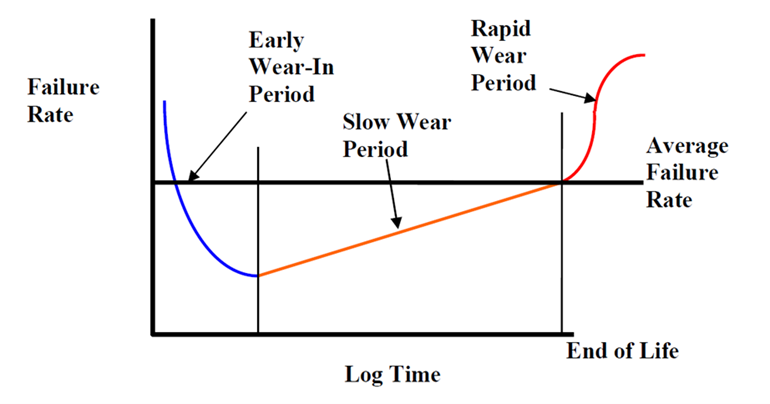
Unfortunately, there is no “standard” methodology that can be applied to mechanical component reliability predictions. Unlike electronic components, most mechanical components and assemblies are wear-dependent over their life cycles, as shown in Figure 2. This limits the accuracy of some of the common reliability prediction models such as the exponential (constant failure rate) reliability method used in MIL-HDBK-217.

MECHANICAL RELIABILITY PREDICTION

It is difficult to model the reliability for the initial “wear-in” period, and for the subsequent “slow wear” period that represents most of the service life. Since the wear-in period is brief, oftentimes models ignore it. Other models treat this complex wear-in and slow wear behavior as constant over a given period of time. An average value is then used in simple reliability models. This prediction approach utilizes generic failure data from a wide range of applications and environments. Average mechanical failure rates are selected from government-published reliability data, such as from NPRD-16, EPRD-14, and NSWC-11.

One challenge in using average values in predicting mechanical reliability is that mechanical components are often operated at a variety of different stress levels over their life cycle, which is different than the constant stresses experienced by electronic components. Think of the varying stresses on the mechanical components in your car’s engine.

Many OEMs are generating significant databases of failure modes, operational stresses, and field reliability data for use in predicting future reliability of traditional product-line items. The major benefit of using OEM data to predict reliability is that many of the variables or applied factors are removed from the analysis computation. Specifically, reliability estimates would presumably be based on field data from parts that have actually had the same (or similar) production processes, operating environments, supplier component parts, etc., to the items under analysis.

However, there are a few issues to consider with this approach. Namely, historical data and related insights lag the development of new components. Also, the inexact science of factoring the subtle differences between the configuration and operation of the fielded item and the new development item, and their impact on system reliability, needs to be addressed.

We recommend employing the following methods when performing mechanical reliability predictions:

Weibull Distribution.   Empirical reliability relationships can be established using limited field (or test) data from representative materials, environment, loading, and configuration. The Weibull distribution is recognized as a practical and useful statistical model of predicted life of a population of items based on field/test data, and best models a non constant failure rate over time. The analysis begins with a review of available data to determine the type of Weibull function to use. If failures exist, the preferred 2-or 3-parameter Weibull function is applied. If no failures have occurred, and there’s no indication of impending failure, then it’s impossible to empirically define the shape factor, Beta (β), which describes the change in failure rate over time. Therefore, data points must be treated as “suspended” data, and a one-parameter Weibull function can be employed with an assumed shape factor (β). A component failure rate can be predicted using the following Weibull function equation:

Where:

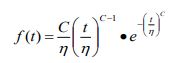
f(t) = Failure rate of component at time t
C = Constant, assumed Weibull shape factor (β)
η = Characteristic life estimated from test data
t = Service life of the end item
e = Mathematical constant (~ 2.71828)

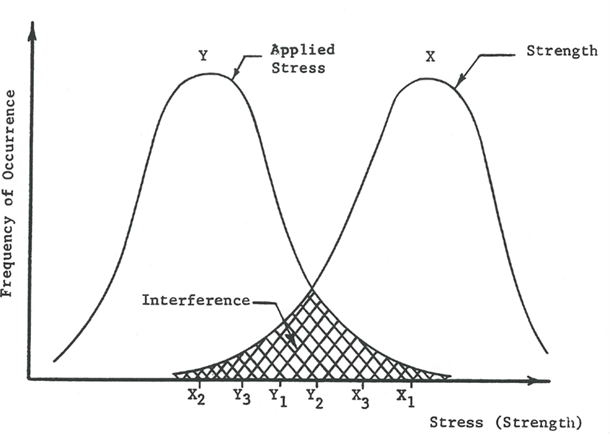
Stress-Strength Interference Method.   The Stress-Strength Interference Method attempts to obtain a point estimate of reliability within the service life of a mechanical component that accounts for the variability of loading and material strength properties. Application of this method requires knowledge of a component’s material characteristics, as well as the stress distribution experienced during operation. The quality of the reliability estimate depends on the accuracy of the material characterization (developed through lab testing) and mechanical loading characterization (developed through finite element modeling). This method treats both stress and material strength as random variables subject to probabilistic scatter. The area of intersection between the distributions of stress and strength is the “interference” and represents the probability of mechanical component failure, as shown in Figure 3.

Physics of Failure.   “Physics of Failure” (POF) is particularly applicable when describing physical, chemical, mechanical, or electrical contributions to degradation of structural material and, eventually, failure. As applied to mechanical reliability, POF offers algorithms (for studied circumstances) that relate degradation functions to reliability parameters. Much the same as Stress-Strength Interference, this approach is predicated on the material and loading characteristics being well understood. Often, this reliability assessment approach has not been fully developed to represent a particular material and loading situation.

The Reliability Engineer must apply an analysis method that best represents the expected failure mechanism for component type and application. It is also important to keep in mind that even if the reliability estimate does not accurately reflect operation, the predicted reliability still serves as a useful measure of the scope of the support system requirements and highlights the reliability drivers to be addressed during design and test to achieve reliability growth.

Article Authored by Stephen Brunner